이건 제가 좀 읽어보고.. 요약본을 올려볼게요! 일단은 이렇게 ^^;;
Weekly Results += 128, Network Weight, Statistics and Nodemap
This is my third week of reporting on the public deployment of Qtum Mainnet Ignition, examining the parameters and performance of the Qtum blockchain. Data sources for this article come from the Qtum Explorer and logging of the qtumd wallet.
Mainnet saw increasing activity this week, with the token swap on Coinone completed. Unique wallet addresses winning block rewards grew to 343 per day, and the network weight peaked up to almost 16 million. The number of Qtum ERC-20 tokens burned reached 41%, up from 26% last week. In addition to the usual staking results charts and graphs, I cover the following topics:
· Errata on target block spacing
· How is network weight calculated?
· Probability and statistics for block rewards (educational)
· The Qtum Nodemap
Network Weight
Network weight increased to a peak of 15,907,217 for block 31,638 on October 22.
Network weight varies dynamically on a block-by-block basis. An example is the network weight for October 19, which varied from a low of 8,060,321 at block 29,312 to a high of 14,589,769 at block 29,710.
Unique Reward Addresses
The network continued to become more diverse with a peak of 343 unique wallet addresses winning block rewards on October 16th. Later in the week, some big wallets joined which reduced this number.
How high could the number of unique reward address per day go? In the extreme with thousands of small wallets, the number of unique reward addresses per day could reach the number of blocks per day. This is unlikely because of random probability (a small wallet could win two block rewards per day) and because of the big wallets hauling in 4 to 20 block rewards a day. Over time, this number could reach the 400 — 450 range. This is a very healthy diversity compared to bitcoin where the top 8 pools win approximately 82% of the blocks.
Transactions Per Day
Transactions per day peaked at 11,036 on October 20 as Coinoners withdrew QTUM from that exchange.
Block Spacing Variation
This week I am able to make a deeper dive into block spacing variation, working with a larger data set of the block spacing for October 15 through October 21[1]. In this week of data there were 9 blocks with more than 20-minute spacing, with the greatest spacing for block 28,632 at 38:06. There were some speedsters on the low end too, with block 30,536 the winner at only a few seconds. Here is a look at the block spacing, for those spacings from 0 to 528 seconds.
A brief explanation about these Excel histogram charts. The x-axis groups the sorted occurrences into “buckets”, for example, the leftmost bar shows that for the bucket of 2 seconds to 17 seconds, there were 455 occurrences.
Next we “zoom in” on the block spacing and look at the occurrences from 0 to 256 seconds. 256 seconds is twice the target block spacing of 128 seconds, and about 85% of the block spacings are within this range. If we plot the results in one second buckets there is a clear 16 second pattern visible.
Occurrences are definitely clustered around 16 second cycles, which I think is related to the Proof of Stake algorithm solving for the next block reward winner (e.g., solving for the kernel hash). The dispersion around these intervals is probably due to the measurement accuracy of my logging (+- 2 seconds) and propagation time through the network.
Annual Return
This week’s annual return chart is corrected for the 128 second target block spacing (see below) which gives first-year total block rewards of 985,550 QTUM[2].
Normalized Weighting for Foundation Wallets
The Foundation vs. private chart below compares the block reward winners each day with a list of 3 dozen Foundation wallet addresses that were active before October 4th. On October 22nd, Foundation wallets were collecting 34% of the block rewards.
The methodology for calculating and charting the normalized Foundation capacity is given in a previous report. This chart attempts to show the total weight of Foundation wallets normalized for changes in network weight. The small sample size of 600 blocks a day causes some randomness for this calculation, but it appears that the Foundation held their mining capacity constant during the week.
Target Block Spacing = 128 seconds for 675 blocks per day
This is a correction to block space timing that I had used in my prior reports, where I had been using return calculations based on “2 minutes” (120 seconds) target block spacing, or 720 blocks per day. The correct target block spacing is 128 seconds (a little longer, and maybe not coincidentally 2 x Blackcoin’s target block spacing)[3]. This means that previous calculations of expected return (using 720 blocks per day) overstated returns by 6.3%. With this corrected value, you can calculate the same “expected time to reward” as the wallet, using your weight and the network weight (more on network weight next), and the formula is:
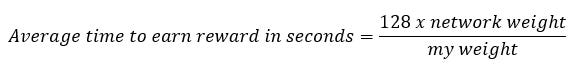
Network Weight
On the QtumNexus Slack this week there was some discussion of the network weight, some of the huge variations we saw, and why this might be happening. I think we have a mental model of “network weight” that is useful, but not grounded in reality (mea culpa, I was previously describing network weight as the sum the mature coins in all staking wallets).
The Qtum network is a peer-to-peer system with the wallets operating independently, and these wallets could not actually know the weight of all the wallets staking on the network. For example, as the network grows to thousands of nodes (wallets), the nodes simply couldn’t collect and process the data, and there is no central server in Patrick’s basement doing the network weight calculation.
What we do have is the blockchain orchestrating everything, with each node tightly coupled to the network through the blocks. Based on the code, each wallet independently calculates the “network weight” based on data from recent blocks using what financial technical analysts would call a simple moving average. This approach somehow captures the weights of the recent block reward winners and crunches them into a meaningful number: the “network weight.”
Understanding how the network weight really works helps explain the variation we see in the network weight, which fluctuates (sometimes almost wildly) on a block-by-block basis. Really big wallets (> 300k QTUM) will cause variations in the moving average when they come online and begin winning block rewards, go offline, or have an unlucky run.
Probability and Statistics for Block Rewards
(Put on your wellies, we are going to wade into some math here. If you don’t want to learn about the probability and statistics behind block rewards, please skip ahead to Nodemap)
Your report writer had some time to think about probability and the distribution of block reward timing this week, as he suffered through a long fallow period for his wallet. Patience is a virtue, and while waiting for block rewards, patience is also a necessity. The wallet gives the expected time to a reward (with the calculation shown above), but I wondered, how long could the wait be?
To answer this question we need some basic probability. First, we consider independent trials, and there have been some questions related to this on the Slack and subreddit this week. Random variables do not have a history because each roll of the dice, spin of the roulette wheel, etc., is an independent trial and the previous results have no influence on the next result. That is why you can’t beat a roulette wheel, slot machine (usually), or lottery (usually) by keeping track of previous results.
The timing for Qtum block rewards does not have a history, and the “time to expected reward” is a calculation of the average time, with no history involved. With PoS staking, rewards do not accrue like they do for pool mining. If your expected time to reward is one day, it doesn’t mean that after one day you will get the reward, it means that on average you will get a reward in one day, but the actual time could be much less or much greater.
Probability of winning
The probability of winning the next block reward is simply your wallet weight, divided by the network weight. Suppose you have a wallet with 1,000 mature coins, and the network weight is 10,000,000, then the formula gives:
Probability values range from 0.0 (not gonna happen) to 1.0 (guaranteed to happen). A probability of 0.0001 means there is 1 chance in 10,000 you will win, or in percentage terms, a 0.01% chance of winning the next block reward.
To calculate the probability of winning a block reward over multiple independent trials, you simply add the probability for each trial:
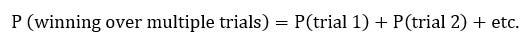
The probability of winning a block reward in one day can be calculated by taking each of the 675 trials in a day and adding them together, or more easily, taking the probability of one trial and multiplying by 675:
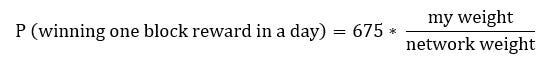
Continuing this example, the probability for a block reward in one day for 1,000 coins, with the network weight of 10,000,000 is 0.675, or 67.5%. To get a probability of 1.0 (the time period where on average, it should happen), divide 1 by 0.675 to get 1.482 days, which the qtum-qt wallet would display (rounding down to 1 day) as
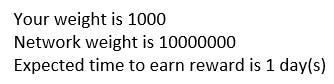
Test your understanding of independent trials: could a wallet win two blocks back-to-back? [4]
Probability of not winning
How can we examine the probability of not winning a block reward over a given period of time, so that we can tell if we should worry when our wallet goes through a fallow period? I should have paid more attention in statistics class, and even though I think the answer lies somewhere with the distribution of interarrival times for Poisson processes[5], I’m going to fall back on the Python script simulator for block rewards that I wrote for the first paper in this series.
At this point in the paper we are switching from the probability calculations above, which are giving “on average” answers, e.g., your expected time (on average) to win a block reward is 1 day. Using statistics, we can get answers like: what percentage of the time will I have to wait 3 days for a block reward?
Using input parameters for the simulator of my weight = 1,000, and a network weight of 10,000,000, I looked at the time between block rewards, which is what an individual wallet would experience. Running through 100 years of rewards (with no yearly compound interest effects) the simulation won 2,449 block rewards, with a median time of 9.90 days. This means that for 50% of the time, the simulation received a block reward before 9.90 days. This also means that for 50% of the time, there was no block reward before 9.90 days.
The resulting chart of “No Reward Before a Time” is given below.
With statistics, we don’t have to say “on average” anymore. We can say, using this chart, that 50% of the time this wallet will not receive a block reward within 9.9 days (point A), and that for 10% of the time this wallet will not receive a block reward within 32.2 days (point B).
To use these results with your wallet, scale the t
2017.10.25 09:58
우리에겐 구글 번역이....